Chiffres significatifs, incertitudes relatives et absolues

Article posté le 26-05-2014 dans la catégorie Maths

Article mis à jour le : 05-05-2022

Comment interpréter la précision des mesures avec les chiffres significatifs, et les incertitudes relatives et absolues.

1- Les chiffres significatifs

On parle de chiffres significatifs pour les chiffres qui composent un nombre et qui ont une importance dans l'évaluation de la mesure qu'il représente.

Exemple : 

• 1,4 -> 2 chiffres significatifs
• 1,40 -> 3 chiffres significatifs
• 0,14 -> 2 chiffres significatifs (le zéro à gauche du premier chiffre ne compte pas)

2- Incertitudes

Quand nous réalisons une mesure, celle-ci est approximative. Ne nous pouvons garantir sa précision. Cela dépend de tellement de facteurs comme l'habileté et l'expérience de la personne qui effectue la mesure, la précision de l'outil utilisé...

Par exemple quand nous mesurons la longueur d'un segment avec une règle, la mesure que nous relevons dépend notamment :

• De la précision (graduation) de la règle
• De la précision du tracé du segment
• De la qualité de notre vue

On parle alors d'erreur : soit la différence entre la mesure et la valeur exacte.

2-A Incertitude absolue

Pour faire simple, l'incertitude absolue est une estimation de l'erreur faite par la personne qui effectue la mesure. Il s'agit de l'écart maximum possible entre donc la mesure, et la valeur exacte.

Usuellement, on appelle :

• X la mesure
• ΔX l'incertitude absolue

Un petit dessin pour mieux comprendre :

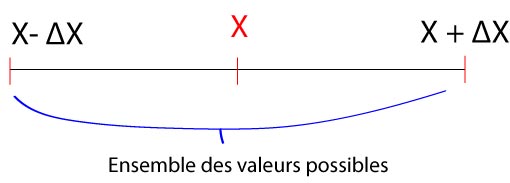
L'incertitude absolue est donc l'erreur maximum possible, exprimée avec les mêmes unites que la mesure, mais elle dépend de la précision de l'outil utilisé pour la mesure. Par exemple : 

•  On estime la vitesse d'une voiture entre 90 et 92 km/h. On peut donc dire qu'elle va à 91 +- 1 km/h

Cependant, l'incertitude absolue est souvent égale à la moitiée du plus petit chiffre significatif. Ce qui signifie que :

• On mesure 19,8 cm avec une règle dont la graduation va jusqu'au millimètre. On peut donc dire que : ΔX = la moitié d'un millimètre  donc 0,5 mm donc 0,05 cm.  On peut dire que la mesure fait 19,8 +- 0,05 cm ou 19,8 +- 5 x 10 ^-2cm
• Une autoroute fait 286 km. Donc elle a une incertitude absolue de 0,5 km

2-B Incertitude relative

On parle d'incertitude relative pour exprimer l'erreur maximum possible en pourcentage de la quantité mesurée ou calculée. Il s'agit simplement du rapport entre l'incertitude absolue et la valeure mesurée :

Exemple :

On mesure avec un chronomètre, ayant une incertitude relative de 0,4%, une durée de 5 secondes. On peut donc retrouver l'incertitude absolue :

A l'inverse, si dès le départ je connais l'incertitude absolue:

Incertitude relative = 0,02 / 5 =  0,004 de l'unité mesurée = 4 x 10^-3 de l'unité mesurée 0,4 x 10^-2 = 0,4 %